Introduction

For spatial data indexing, Quad-Trees have carved out an essential niche, providing simplified, efficient, and balanced solutions in the field of geospatial data management. This tree data structure is highly useful in applications like image processing and computational geometry. To fully appreciate and employ Quad-Trees, it's essential to understand their functionality, benefits, and limitations. This article presents a comprehensive overview of the Quad-Tree geospatial data structure.

What is Quad-Tree?

Quad-Tree, as the name implies, is a tree data structure where each internal node has exactly four children: north-west, north-east, south-west, and south-east. Quad-Trees are primarily used to partition a two-dimensional space by recursively subdividing it into four quadrants or regions. Introduced by Finkel and Bentley in 1974, Quad-Trees gained prominence in fields like computer graphics and GIS for their ability to quickly locate points in a plane.

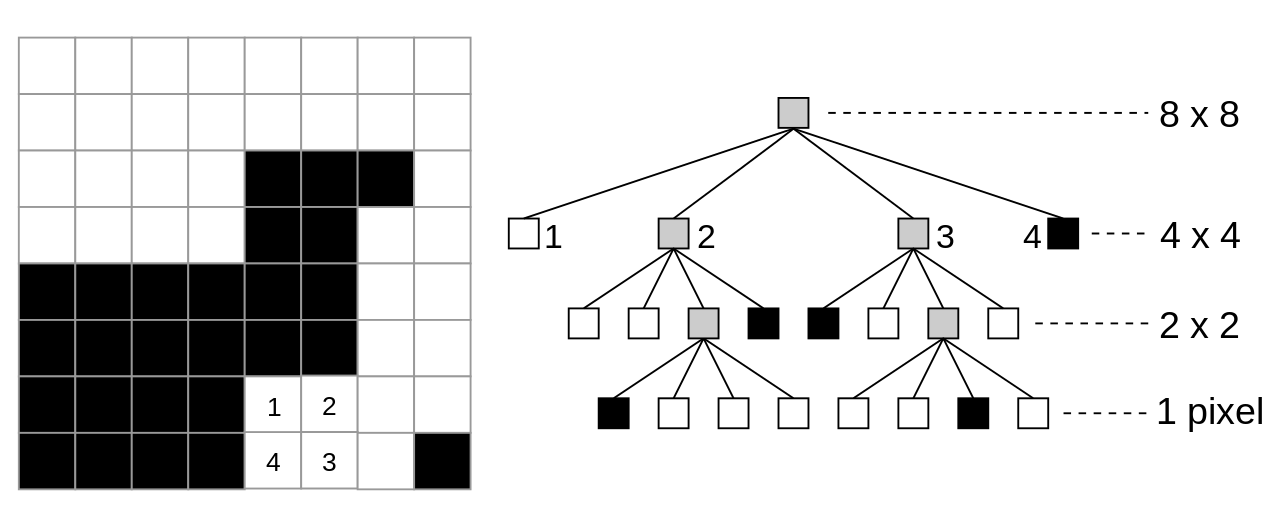
How Does Quad-Tree Work?

The root node of a Quad-Tree represents the entire area under consideration. As we move down the tree, the area gets divided into four equal quadrants, and each quadrant corresponds to a child node. This subdivision continues until a threshold condition is met, usually when a node contains only one data point, or when it reaches a predetermined depth.

Imagine a map divided into four parts. If a region contains significant data (like cities, terrain, etc.), it is further split into four smaller parts. This subdivision continues until we reach an area that contains only one piece of significant data or none.

Benefits of Quad-Tree

1. Speed and Efficiency: Quad-Trees facilitate fast region queries and updates as they reduce the search space considerably with each level.
2. Adaptive Resolution: Quad-Trees offer an adaptive resolution as different regions of space can be represented at different levels of detail. For example, a region with a high concentration of data points can be subdivided more than a region with few data points, offering a higher resolution where needed.
3. Intuitive and Easy to Implement: Quad-Trees follow a simple rule for subdivision, and hence are relatively easier and more intuitive to implement than other spatial data structures.

Limitations of Quad-Tree

1. Inefficient with Irregular Data: Quad-Trees may not be efficient when data is distributed irregularly, leading to trees that are deeper on one side. This could potentially result in longer query times.
2. Difficulty Handling Dynamic Data: Quad-Trees are not particularly well-suited for handling data that changes frequently (dynamic data). Adding and removing points can cause significant changes to the structure of the tree, potentially leading to a high computational cost.
3. Not Optimal for High-Dimensional Data: Quad-Trees are ideal for two-dimensional data. However, as the number of dimensions increases, the number of children for each node increases exponentially, making the tree highly inefficient.

Conclusion

Despite some limitations, Quad-Trees serve as a powerful tool in spatial data indexing, particularly in dealing with two-dimensional data. They offer quick spatial queries and can adapt to different data densities, making them useful in various applications. When choosing the right tool for geospatial data management, it's crucial to consider both the benefits and limitations of Quad-Trees. To broaden your knowledge of geospatial data structures, don't forget to check out our comprehensive guide on other geospatial data structures used in the field.