Introduction

Space-filling curves provide an ingenious solution to multi-dimensional data handling, playing a significant role in geospatial data structures. Their unique property of preserving locality and converting multi-dimensional data into a one-dimensional form offers various advantages in geospatial data processing. This article explores the functionality, benefits, and limitations of Space-Filling Curves in managing geospatial data.

What are Space-Filling Curves?

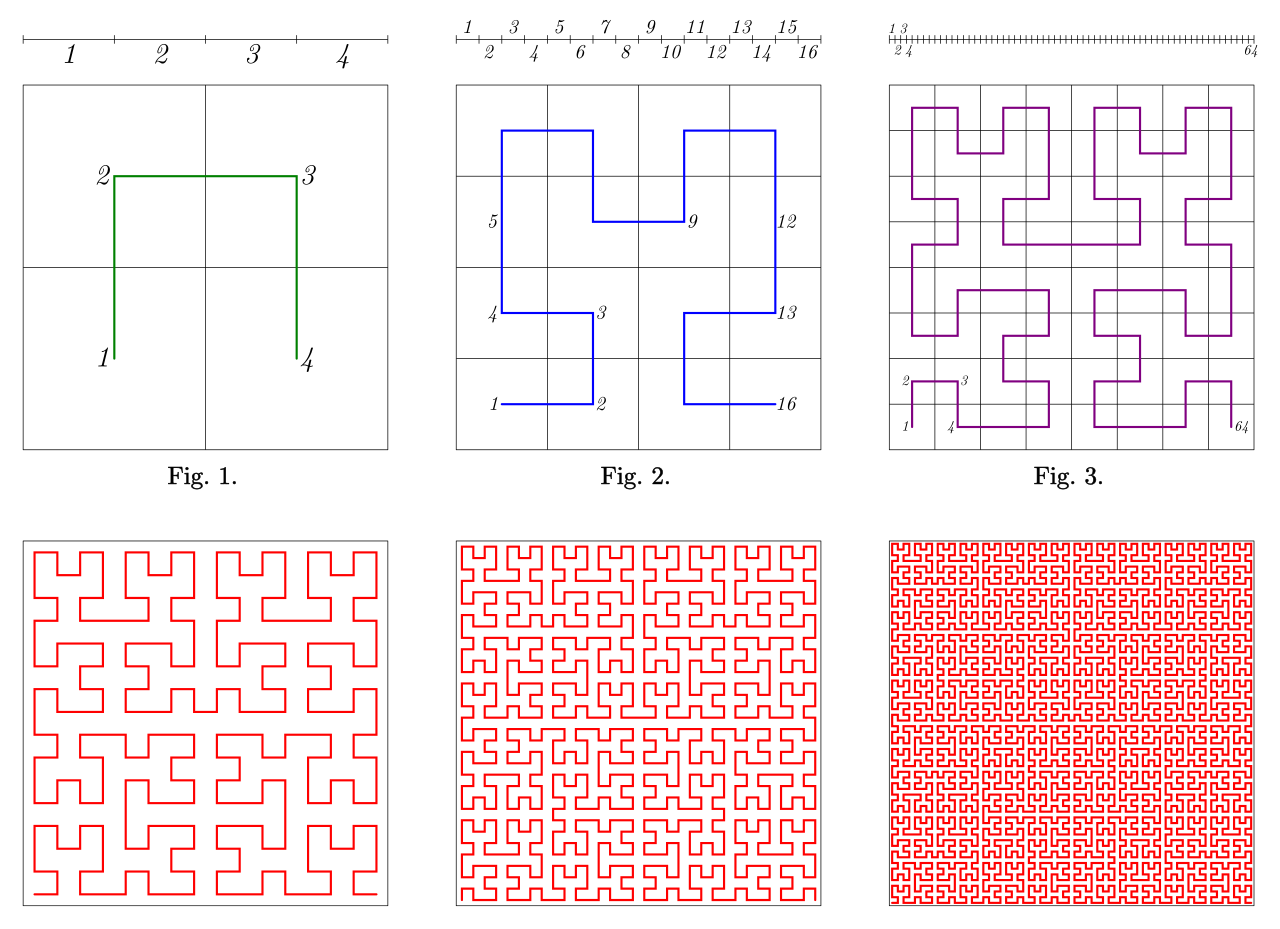
Space-filling curves are continuous curves that pass through every point in a multi-dimensional grid exactly once. These curves can map a multi-dimensional space onto a one-dimensional space, preserving the spatial locality of the data points. Popular space-filling curves include the Hilbert Curve, Peano Curve, and Z-order (or Morton) Curve.

How Do Space-Filling Curves Work?

Space-filling curves traverse through each cell of a multi-dimensional grid exactly once, converting multi-dimensional data into a one-dimensional sequence. By maintaining the locality of data points during this conversion, the curves enable efficient spatial and range queries. These curves can be thought of as a road map that a very meticulous delivery person might follow: starting at one end of their territory, they cover every single location (or "cell") exactly once without any backtracking, until the entire territory is covered.

Think of a space-filling curve as a very careful gardener who has to water every plant in a large rectangular garden exactly once. The garden is divided into smaller square patches, each containing a single plant. The gardener starts at one corner of the garden and walks in a continuous path that winds back and forth, up and down, covering every small patch without leaving any out or watering any twice. Regardless of the garden's size, the gardener's path is unbroken and never crosses itself, ensuring each plant gets watered exactly once. Similarly, a space-filling curve "visits" every point in a multi-dimensional space without skipping or repeating any point, providing a method to traverse through all the data points in a systematic and efficient way.

Benefits of Space-Filling Curves

1. Locality-Preserving: One of the primary advantages of Space-Filling Curves is their ability to preserve spatial locality. This feature ensures that data points close to each other in the multi-dimensional space remain close in the one-dimensional sequence, enhancing the efficiency of range queries.

2. Simplicity: The concept and construction of Space-Filling Curves are straightforward. This simplicity allows for easy implementation and use in a variety of applications.

3. Reduced Dimensionality: By converting multi-dimensional data into one-dimensional data, Space-Filling Curves reduce the complexity associated with handling multi-dimensional data.

Limitations of Space-Filling Curves

1. Limited Precision: The precision of mapping is limited to the granularity of the grid used. The finer the grid, the more precise the mapping, but this comes at the cost of increased computational complexity and storage requirements.

2. Complexity of Higher-Order Curves: Constructing higher-order space-filling curves can be complex and computationally intensive. This complexity grows with the increase in dimensionality and resolution of the grid.

3. Partial Coverage: When dealing with a query range that does not align perfectly with the grid's cells, space-filling curves may return extra points that are not in the query range. This necessitates an additional filtering step to remove these extra points.

Conclusion

Space-Filling Curves offer a unique approach to handling geospatial data by reducing dimensionality while preserving spatial locality. Although they have some limitations, like precision constraints and complexity of higher-order curves, their benefits like locality preservation, simplicity, and reduced dimensionality make them a valuable tool in geospatial data management. As with all tools, a thorough understanding of both their advantages and limitations is crucial when deciding on the best tool for your geospatial data needs. For a more extensive exploration of spatial data management, check out our comprehensive guide on geospatial data structures.